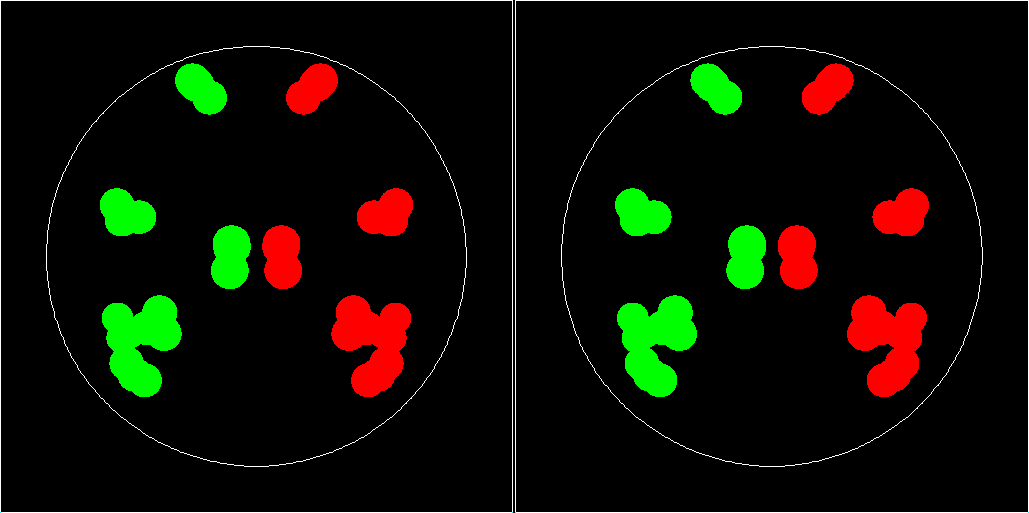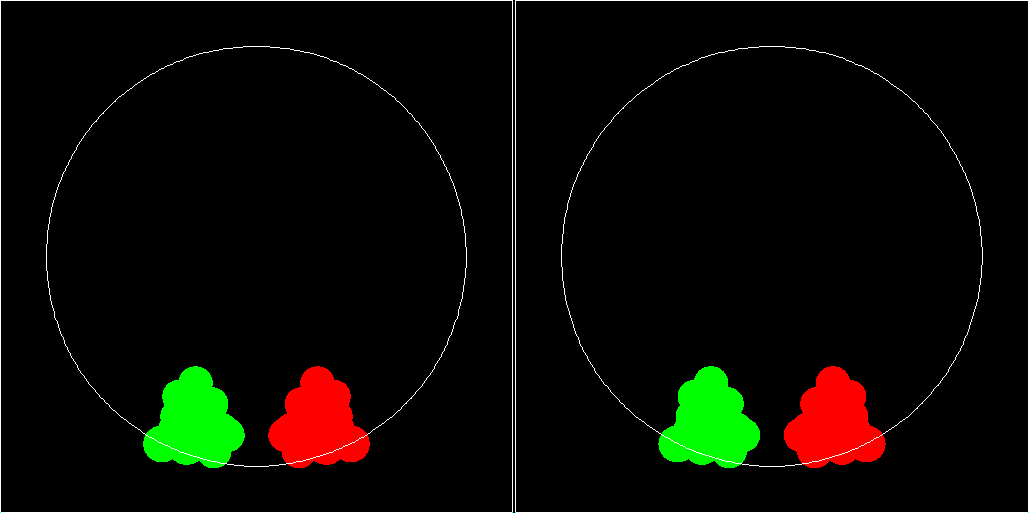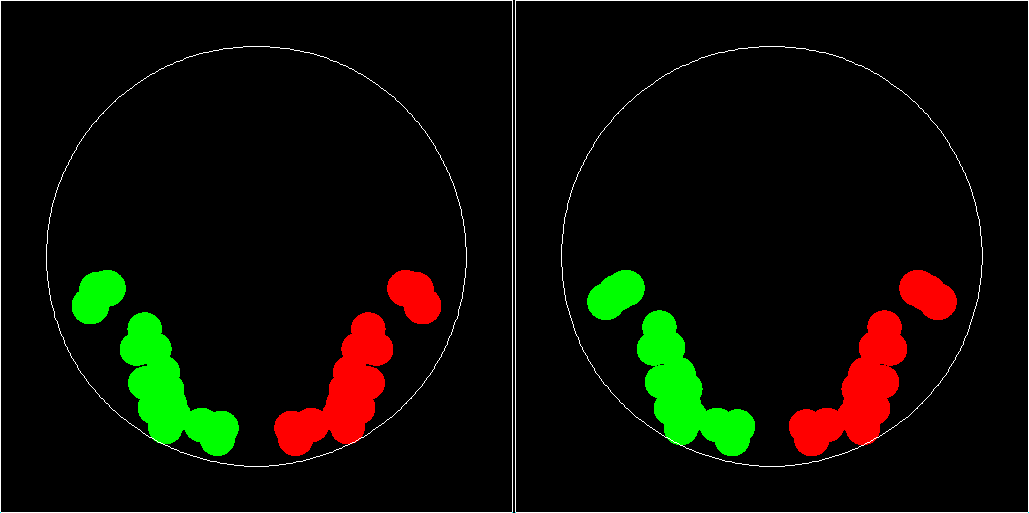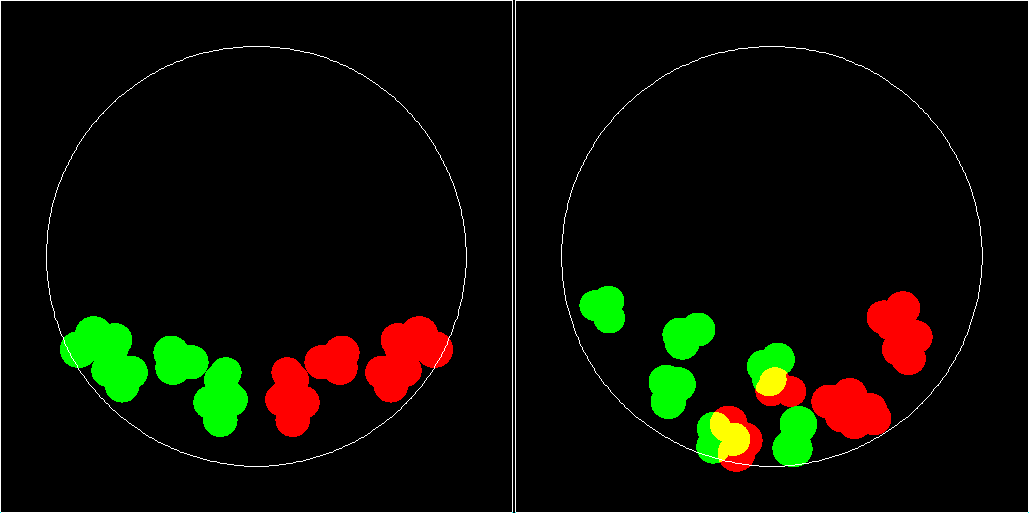

Left image: computation done with 32 digital places numerical precision. Right image: 10 digital places. See article8 for an explanation of polyspherical particles and a robust and efficient computational implementation of their dynamics. Towards the end of the simulation the left and the right image begin to look different and finally in the right image (the one which was computed with the lower precision) the mirror symmetry between the red and green particles gets lost. The system, which is here shown twice for comparison of two computations, consists of 12 particles which which make a free fall in a cylindrical drum with a closing lid at both ends. Each particle consists of three spherical components which strongly overlap. Six of the particles are generated by a a procedure which involves random variations of the parametes (such as radii of the spherical componets). The other six particles are defined as mirror images of the original particles. Also the initial placement of the particles shows this mirror symmetry, as does the containing drum, and the homogeneous gravitation field which causes the motion of the particles, which are initially at rest. Under these conditions the exact solution of the equation of motion (we use simple elastic forces between the spherical components of the polyspherical particles and between particles and drum) remains mirror symmetric for all times. Numerical errors destroy this symmetry slowly but effective. The rotational degree of freedom lets the effect of a collision depend much more sensitively on the collision geometry than it would be the case for simply spherical particles. The images shown are parallel projections along the drum's axis so that the mirror symmetry under consideration reflects itself in the left to right mirror symmetry of the green area (original particles) and red area (particles with mirror symmetric initial condition). See also the final section of the rational for my multiple precision Ruby class R . Total energy is very well conserved in both computations, with only tiny oscillations and no detectable trend. This is a beneficial property of the integrator which is used here. Less robust integrators distroy the mirror symmetry much earlier. Remark: When, as a student, I had an awesome look into the 10 digit logarithmic tables by Peters and Bauschinger, I did not anticipate that I would ever consider 10 digits 'low numerical pecision'.